해당 내용은 coursera Andrew Ng교수의 Machine Learning강의 노트 정리
Examples and Intuitions
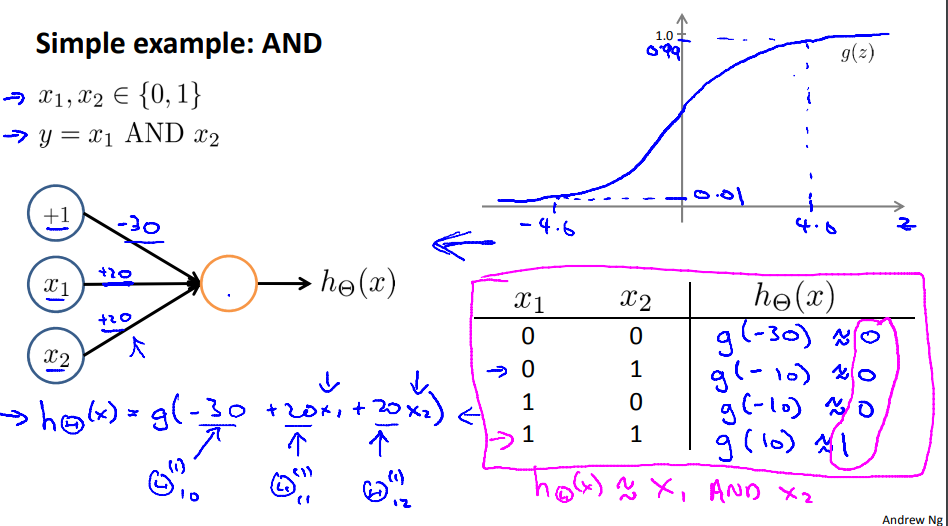
$x_1 AND x_2$를 예측하는 간단한 neural network을 예시로 들어보면 $x_1$과 $x_2$가 1일 경우 true인 논리연산자이다 예를 들어 만일 bias 값이 30이고 $x_1$과 $x_2$의 weight가 20이라고 할 때 $h_{\theta}(x) = g(-30+20x_1+20x_2)$가 된다. Activation function은 sigmoid일 때 $x_1=x_2=1$인 경우만 $h_{\theta}(x) \approx 1$이 된다.
$$ \begin{align*}& h_\Theta(x) = g(-30 + 20x_1 + 20x_2) \newline \newline & x_1 = 0 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-30) \approx 0 \newline & x_1 = 0 \ \ and \ \ x_2 = 1 \ \ then \ \ g(-10) \approx 0 \newline & x_1 = 1 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-10) \approx 0 \newline & x_1 = 1 \ \ and \ \ x_2 = 1 \ \ then \ \ g(10) \approx 1\end {align*} $$
여기서 AND 게이트 대신 simple NN으로 연산을 하였고 다른 형태의 logical 연산에도 이용할 수 있다. OR 연산을 예시로 하면 $x_1, x_2$는 AND연산에서의 weight와 동일하게 20이라고 하고 bias는 -10으로 주어졌을 때 다음과 같은 결과가 나타난다.
$$ \begin{align*}& h_\Theta(x) = g(-10 + 20x_1 + 20x_2) \newline \newline & x_1 = 0 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-10) \approx 0 \newline & x_1 = 0 \ \ and \ \ x_2 = 1 \ \ then \ \ g(10) \approx 1 \newline & x_1 = 1 \ \ and \ \ x_2 = 0 \ \ then \ \ g(10) \approx 1 \newline & x_1 = 1 \ \ and \ \ x_2 = 1 \ \ then \ \ g(30) \approx 1\end {align*} $$
$(NOT\ x_1)AND(NOT \ x_2)$의 게이트를 생각해 본다면 $x$가 1이 아닌 경우 참이 된다.
$$ \begin{align*}& h_\Theta(x) = g(10 - 20x_1 -20x_2) \newline \newline & x_1 = 0 \ \ and \ \ x_2 = 0 \ \ then \ \ g(10) \approx 1 \newline & x_1 = 0 \ \ and \ \ x_2 = 1 \ \ then \ \ g(-10) \approx 0 \newline & x_1 = 1 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-10) \approx 0 \newline & x_1 = 1 \ \ and \ \ x_2 = 1 \ \ then \ \ g(-30) \approx 0\end {align*} $$

이 모든 과정을 하나로 하여 activation layer 2의 1번째 노드를 AND 로직 형태로 2번째 노드를 XNOR형태로 마지막 ouput을 OR형태로 설계할 수 있다.
Multiclass Classification

multiclass classification 의 경우 $y\in \{1, 2, 3, 4\}$가 아닌 $hΘ(x)=[0010]$의 형태로 나타내어진다.
Refrenece
Machine learning , Coursera, Andrew Ng