$u=\begin{bmatrix}u_1\\u_2\end{bmatrix}$ , $v=\begin{bmatrix}v_1\\v_2\end{bmatrix}$의 두개의 vector가 있을 때

$u^Tv = [u_1 \ u_2]\begin{bmatrix}v_1\\v_2\end{bmatrix}=u_1v_1+u_2v_2=p*\lVert u \rVert$, p는 v를 u 에 정사영 시킨 길이를 나타낸다.
$\lVert u \rVert$은 vector u 의 길이. $= \sqrt{u_1^2+u_2^2}$
SVM Decision boundary 에서 $\theta$가 2개라고 가정
p는 vector $\theta$에 $x$를 정사영 시킨 값.

$$ min_{\theta} \frac{1}{2} \sum_{j=1}^{n}\theta_j^2 \\=\frac{1}{2}(\theta_1^2+\theta_2^2)\\=\frac{1}{2}(\sqrt{\theta_1^2+\theta_2^2})^2\\=\frac{1}{2}\lVert \theta \rVert ^2\\st \ \ \theta^Tx^{(i)} \ge1 \ \ \ if \ \ y^{(i)}=1 \\ \ \ \theta^Tx^{(i)} \le -1 \ \ \ if \ \ y^{(i)}=0\\ \Rightarrow \\ p^{(i)} \cdot \lVert \theta \rVert \ge1 \ \ \ if \ \ y^{(i)}=1 \\ \ \ p^{(i)} \cdot \lVert \theta \rVert \le -1 \ \ \ if \ \ y^{(i)}=0\\ $$

Kernel
non-linear decision boundary를 예측할때

$y=1 \ \ \ \ if \ \ \ \ \theta_0 +\theta_1x_1+\theta_2x_2+\theta_2x_1x_2+\theta_4x_1^2+\theta_5x_2^2 + ... \ge0$ 일 때
$\Rightarrow \theta_0 +\theta_1f_1+\theta_2f_2+\theta_2f_3+...$
$f_1 = x_1,\ \ f_2=x_2,\ \ f_3=x_1x_2,\ \ f_4 = x_1^2 ...$ 이다.

$l^{(1)}, \ \ l^{(2)},\ \,l^{(3)}$는 landmark로 주어진 x에 대해 새로운 feature에 의존한 proximity임.
$f_1 = similarity(x, l^{(1)}) = exp(- \frac{\lVert x - l^{(1)}\rVert ^2}{2 \sigma^2})$
$f_2 = similarity(x_1, l^{(2)}) = exp(- \frac{\lVert x - l^{(2)}\rVert ^2}{2 \sigma^2})$
$f_3 = similarity(x, l^{(3)}) = exp(- \frac{\lVert x - l^{(3)}\rVert ^2}{2 \sigma^2})$
similarity 는 kernal이라고 하고 exponential을 쓰기때문에 Gaussian kernal이라고 함
$$ f_1 = similarity(x, l^{(1)}) = exp(- \frac{\lVert x - l^{(1)}\rVert ^2}{2 \sigma^2})\\ If \ \ \ x\approx l^{(1)}:\\f_1 \approx exp(- \frac{0 ^2}{2 \sigma^2})\approx 1\\If \ \ \ x \ \ \ if\ far\ from \ \ l^{(1)}:\\f_1 \approx exp(- \frac{(large \ number)^2}{2 \sigma^2})\approx 0 $$
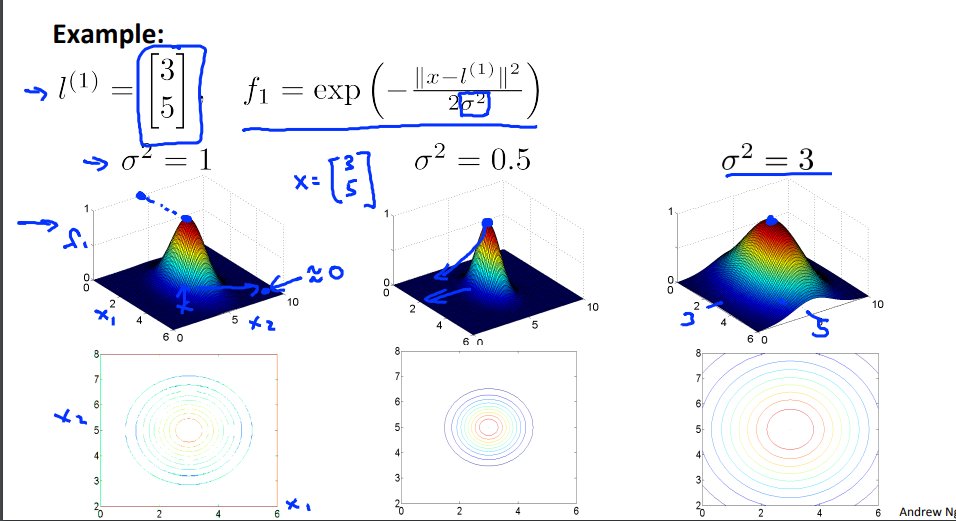
$\sigma$는 분포가 얼마나 퍼져 있는지를 알수 있는데 $\sigma^2=0.5$이면 분포가 좀더 작아지고 $\sigma^2=3$이라면 분포가 넓게 퍼진 형태가 되는 것을 확인할수 있음.
그렇다면 $l$은 어떻게 구해야 할까?
$(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})$ 이 주어지고 $l^{(1)}=x^{(1)},l^{(2)}=x^{(2)},...,l^{(m)}=x^{(m)}$으로 하면 주어진 $x$에 대해
$$ f_1 = similarity(x, l^{(1)})\\f_2 = similarity(x, l^{(2)}).... $$
즉 $f= \begin{bmatrix} f_0 \\ f_1\\ f_2\\...\\f_m \end{bmatrix}$ $f_0 =1$ 이고 training $(x^{(i)},y^{(i)})$의 예를 들면
$$ f_1^{(i)} = sim(x^{(i)},l^{(1)})\\f_2^{(i)} = sim(x^{(i)},l^{(2)})\\...\\f_i^{(i)} = sim(x^{(i)},l^{(i)})=exp(-0/2 \sigma^2)=1\\f_m^{(i)} = sim(x^{(i)},l^{(m)}) $$
주어진 $x$에 대해 $f$를 계산 하는데 $"y=1" \ \ \ if \ \ \theta^Tf \ge0$를 예측한다.
$min_{\theta} C \sum_{i=1}^{m} y^{(i)}cost_1(\theta^Tf^{(i)})+(1-y^{(i)})cost_0(\theta^Tf^{(i)})+\frac{1}{2}\sum_{i=1}^{m} \theta_j^2$
SVM의 파라미터 $C (=\frac{1}{\lambda})$, $\sigma^2$
Large $C$ : Lower bias, high variance.
Small $C$ : Higher bias, low variance
Large $\sigma^2$ : feature $f_i$가 더 smooth하고, High bias, lower variance
Small $\sigma^2$ : feature $f_i$가 덜 smooth하고 Lower bias, higher variance
Logistic regression vs SVMs
n = number of feature, m= number of training example 일때
- 만일 $n\ge m$ [n =10,000, m= 10 ~1000]일때 → Logistic regress 이나 SVM without a kernel [linear kernel]을 사용
- $n$이 적고, $m$이 적당수 있을때 [n= 1~1000, m= 10~10,000] → SVM with Gaussian kernel
- $n$이 적고 $m$이 많으면 [n= 1~1000, m= 50,000+] → 더 많은 feature를 추가하거나 생성하여 logistic regression or SVM without a kernel
- Neural network은 모든 경우에 적용 가능 하지만 트레이닝이 느릴수 있음